You cannot submit for this problem because the contest is ended. You can click "Open in Problem Set" to view this problem in normal mode.

令人遗憾的是，L是直角。

题目描述

野豌豆非常喜欢钝角，他常常喜欢数平面上任选三个点能否组成钝角三角形，而每当野豌豆发现一个从未发现过的钝角三角形的时候，他就会获得这个三角形面积两倍的满意值。

现在给定二维平面内的$n$个点$(x_i,y_i)$，请问野豌豆最多可以获得多少满意值。

输入格式

输入第一行仅包含一个正整数$T(1\le T\le1000)$，表示数据组数。

对于每组测试数据，第一行包含一个正整数$n(3 \le n \le 1000)$表示平面上总共有$n$个点。

第$i+1$行包含两个正整数$(x_i,y_i)$，表示第$i$个点的坐标，保证$1\le x_i,y_i\le 10000$，且对于$1\le i,j\le n,i\neq j$，保证$(x_i,y_i)\neq(x_j,y_j)$。

输出格式

对于每组测试数据，输出一行一个正整数$S$，为野豌豆最多可以获得的满意值。

样例

3
4
5 7
9 8
2 10
4 2
6
6 8
4 9
9 10
8 2
3 8
9 4
10
3 3
2 4
1 2
6 4
9 2
8 9
4 4
6 3
7 7
9 4

52
145
660

数据范围

对于$30\%$的数据，有$3\le n \le 300$，且$\sum n\le 600$。

对于另外$30\%$的数据，保证任意三点不共线。

对于$100\%$的数据，$1\le T\le 1000$，$3\le n \le 10^3$，$3\le\sum n\le 2\times10^3$，$1\le x_i,y_i\le 10^4$，且保证任意两点不相等。保证答案一定为整数。

提示

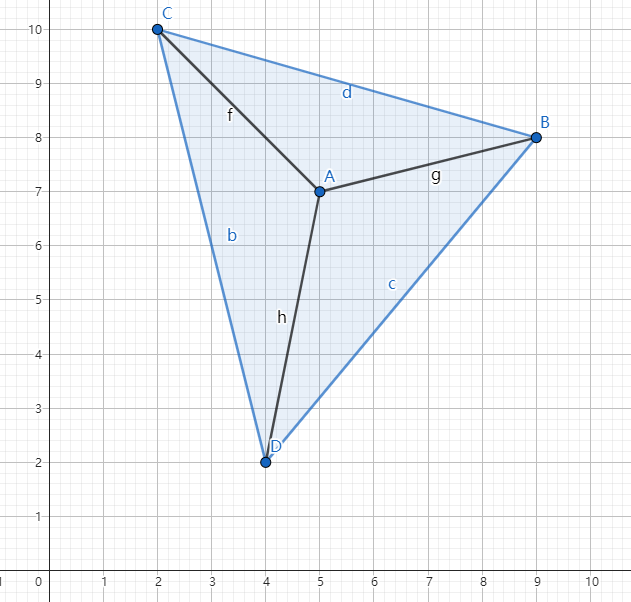
对于样例中第一组数据中四个点的坐标如图所示，其中$\triangle ABC$，$\triangle ABD, \triangle ACD$为钝角三角形，而$\triangle BCD$为锐角三角形。

又因为$S_{\triangle ABC}=7.5,S_{\triangle ABD}=9.5,S_{\triangle ACD}=9$， 最后野豌豆可以获得的满意值等于$S=2S_{\triangle ABC}+2S_{\triangle ABD}+2S_{\triangle ACD}=52$。