本题并不需要你真正解决这个问题。请灵活运用本次比赛的赛制。

题目描述

众所周知，The First Island of Solitude的时代之树能够自动生长。

在一开始，这颗树位于星球的中央。第1秒后，它生长成为一个小树枝，有了首尾两端。

第2秒后，它的首尾两端会各自生长出一个小树枝，与最开始的树枝保持垂直。每个小树枝的长度都完全相同，且之后也会保持一致。

第3秒后，新的小树枝的首尾两端又生长出小树枝。但是，在第4秒时，由于之前有两对树枝的端点重合，重合的位置无法生长出新的小树枝，所以第4秒后，只有没有重合的那些端点生长出了小树枝。

下面的图表示了第1秒到第10秒时这棵树的生长状态。

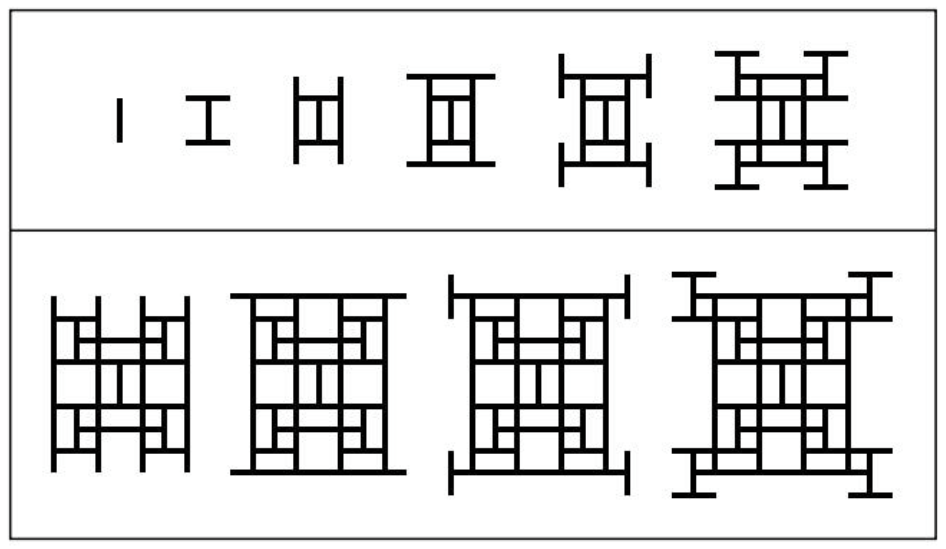
现在，大卫，作为数据结构大师，想要溯源时代之树——也就是你——的变化，因此，他想知道你在一些特定时间的生长状态。

输入格式

输入第一行包含一个整数$q$，表示大卫的询问次数。

接下来$q$行，每行包含一个整数$x$，表示大卫想知道你在第$x$秒后的生长状态。

输出格式

输出共$q$行，每行包含一个整数，表示你在第$x$秒时的树枝个数对998,244,353取模的结果。

样例

7
1
10
100
256
10492
7777777
998244353

1
55
4903
43691
53486507
836625110
836116642

数据范围

对于$100\%$的数据，$1\le q\le 10^5,1\le x\le 2\times 10^9$。

提示

本题的样例输入非常丰富，你可以自由选择其中的部分进行测试。

由费马小定理可得，质数模数意义下的分数

$$\frac1a\equiv a^{p-2}\pmod p$$

特别地，

$$\frac13\equiv332748118\pmod{998244353}$$

如果你对本题没有什么思路，这里可以给你通向AC的提示：

oeis.org是一个用来查询数列规律的网站。如果你已经知道了本题前10分的答案，你可以试着将数字输入这个网站，寻找可能的规律。希望你获得成功。